sorting

Sorting Techniques

CSL 102; Data Structures; IIIT Nagpur; Created by: Dr. Aniket Pingley

Selection Sort

This way of sorting is simplest to imagine. We tend to utilize the principle of selection sort in our day-to-day lives. Assume that we wish to sort a series of values in ascending order. Intuitvely, we will first traverse through an array an select the smallest element and keep it aside. From the remaining elements in the array we will again repeat the steps to find and keep the smallest element aside.

Example of Selection Sort:

Conside the following array consisting of 6 elements: [23, 4, 56, 1, 78, 2]

Step 1: Set starting index = 0 and find the index at which the smallest element is located. In this case 1 is located at index 3.
Step 2: Swap elements at starting index and index 3. The modified array is [1, 4, 56, 23, 78, 2]
Step 3: Increment the starting index by 1. Now the subarray to consider indexes from 1 through 5.
Step 4: The element 2 at index 5 is the smallest. Swap the elements at index 1 and index 5. The modified array now is [1, 2, 56, 23, 78, 4]
.....
.....
Repeat the steps until the starting index equals to 5 (last index)

The following flowchart demonstrates the flow of selection sort algorithm/method.

Link to animation for selection sort - https://yongdanielliang.github.io/animation/web/SelectionSortNew.html


  void selectionSort(int arr[], int n){
    int minIdx = 0;
    for (int i = 0; i < n-1; i++){
        minIdx = i;
        for (int j = i+1; j < n; j++){
          if (arr[j] < arr[minIdx]){
            minIdx = j;
            }
        }
        swap(&arr[minIdx], &arr[i]);
      }
  }

Bubble Sort

Bubble sort is a simple sorting algorithm that repeatedly iterates through an array, compares adjacent elements and swaps them if they are in the wrong order (assume ascending). The iteration through the array is repeated until the array is sorted.

Example of Bubble Sort and Flowchart:

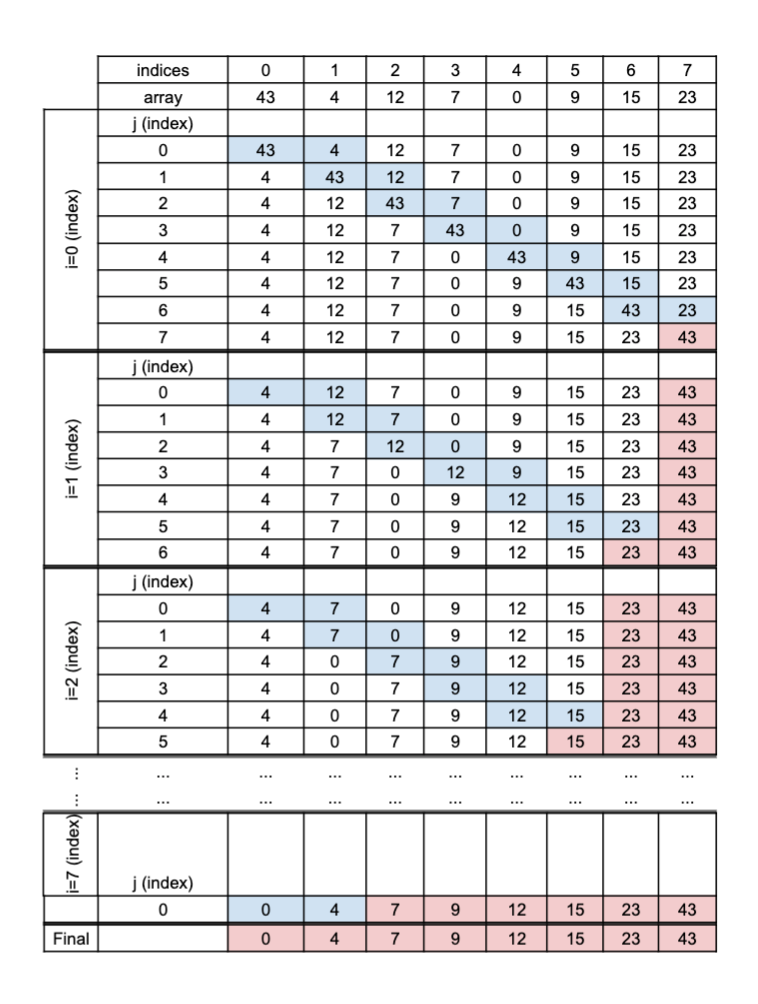
Link to animation for bubble sort - https://yongdanielliang.github.io/animation/web/BubbleSortNew.html


  void bubbleSort(int arr[], int n){
    for (int i = 0; i < n-1; i++){	
	    for (int j = 0; j < n-i-1; j++){
		    if (arr[j] > arr[j+1]){
			    swap(&arr[j], &arr[j+1]);
            }
        }
    }
  }

Insertion Sort

Insertion sort works similar to the way people sort playing cards in their hands. To sort an array of size n in ascending order:

Step 1: Iterate from arr[1] to arr[n] over the array.

Step 2: Compare the current element (key) to its predecessor (element at the previous index).

Step 3: If the key element is smaller than its predecessor, compare it to the elements before. Move the greater elements one position up to make space for the swapped element.

Step 4: Repeat until the iteration reaches the last index of the array.

Example of Insertion Sort and Flowchart:

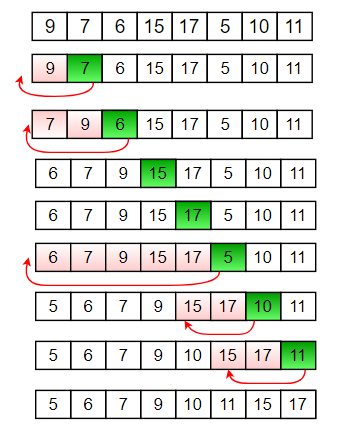Image source: GeeksForGeeks

Link to animation for insertion sort - https://yongdanielliang.github.io/animation/web/InsertionSortNew.html


  void insertionSort(int arr[], int n){
	int key = 0;
    	int j = 0;
	for (int i = 1; i < n; i++) {
	   key = arr[i];
	   j = i - 1;

	   while (j >= 0 && arr[j] > key) {
		arr[j + 1] = arr[j];
		j = j - 1;
	   }
	   arr[j + 1] = key;
	}
   }

Merge Sort

The aforesaid sorting techniques require nearly n² number of steps for input size n. Merge Sort technique is comparitvely more efficient. Similar to Binary Search it is a Divide and Conquer algorithm. To this end, it divides the input array into two halves. Each half is sorted by recursively dividing them individually into two halves. Once the entire array is divided into subarrays of size 1, they are merged into two sorted (ascensding) halves. Described below is the algorithm for merge sort technique.

merge_sort(arr[], left_index, right_index)

If right_index > left_index

Step 1: Find the middle point to divide the array into two halves:
Step 2: Call merge_sort for first half:
Step 3: Call merge_sort for second half:
Step 4: Merge the two halves sorted in step 2 and 3:

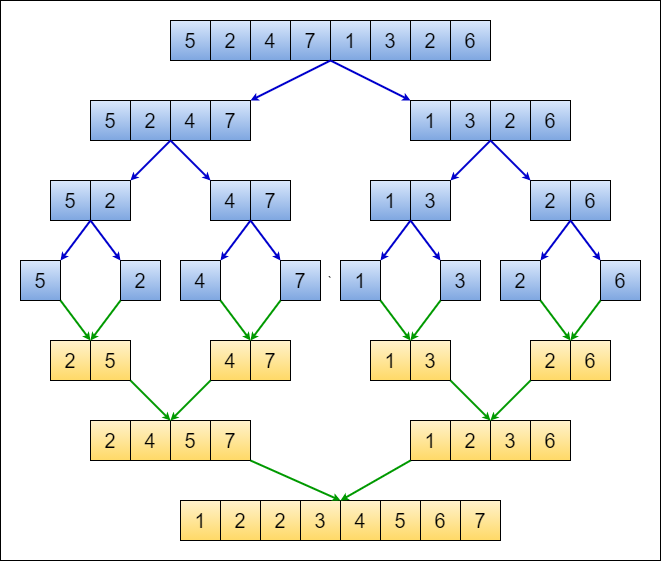Image source: https://levelup.gitconnected.com/

The number of steps required for merge sort for input size n is:

Recursive splitting of array: log₂(n)
Merging of sorted arrays: log₂(n)
Comparison of values at every step: n
Total steps = log₂(n) + log₂(n) * n = nlog₂(n)

Link to animation for Merge sort - Link to hackerearth.


  void merge(int arr[], int left_index, int middle_index, int right_index)
  {
    int sz_left_arr = middle_index - left_index + 1;
    int sz_right_arr = right_index - middle_index;
  
    /* create temporary arrays */
    int left_arr[sz_left_arr], right_arr[sz_right_arr];
  
    /* Copy data to left_arr[] and right_arr[] */
    for (int i = 0; i < sz_left_arr; i++)
      left_arr[i] = arr[left_index + i];
  
    for (int j = 0; j < sz_right_arr; j++)
      right_arr[j] = arr[middle_index + 1 + j];
  
    int i, j, k;
    /* Merge the temp arrays back into arr[l..r]*/
    i = 0; /* starting index of left_arr */
    j = 0; /* starting index of right_arr */
    k = left_index; /* starting index of merged subarray */
    while (i < sz_left_arr && j < sz_right_arr) {
      if (left_arr[i] <= right_arr[j]) {
        arr[k] = left_arr[i];
        i++;
      }
      else {
        arr[k] = right_arr[j];
        j++;
      }
      k++;
    }
  
    /* Copy the remaining elements of left_arr[], if there
    are any */
    while (i < sz_left_arr) {
      arr[k] = left_arr[i];
      i++;
      k++;
    }
  
    /* Copy the remaining elements of right_arr[], if there
    are any */
    while (j < sz_right_arr) {
      arr[k] = right_arr[j];
      j++;
      k++;
    }
  }
  
  void merge_sort_func(int arr[], int left_index, int right_index)
  {
    if (left_index < right_index) {
      int middle_index = (left_index + right_index) / 2;
  
      /*recursively sort first and second halves*/
      merge_sort_func(arr, left_index, middle_index);
      merge_sort_func(arr, middle_index + 1, right_index);
  
      merge(arr, left_index, middle_index, right_index);
    }
  }

Quick Sort

Similar to the Merge Sort technique, Quick Sort employs the Divide and Conquer algorithm. To this end, it picks an element as pivot and partitions the given array around the picked pivot. Each partition is then recursively processed by further partitioning (into subpartitions) around a newly selected pivot (from the partition). The left subpartition will have elements smaller than the pivot. The right subpartition will have elements greater than the pivot.

The pivot can be selected in multiple ways:

Pick first element
Pick last element (avoids 1 extra swap)
Pick a random element
Pick median element

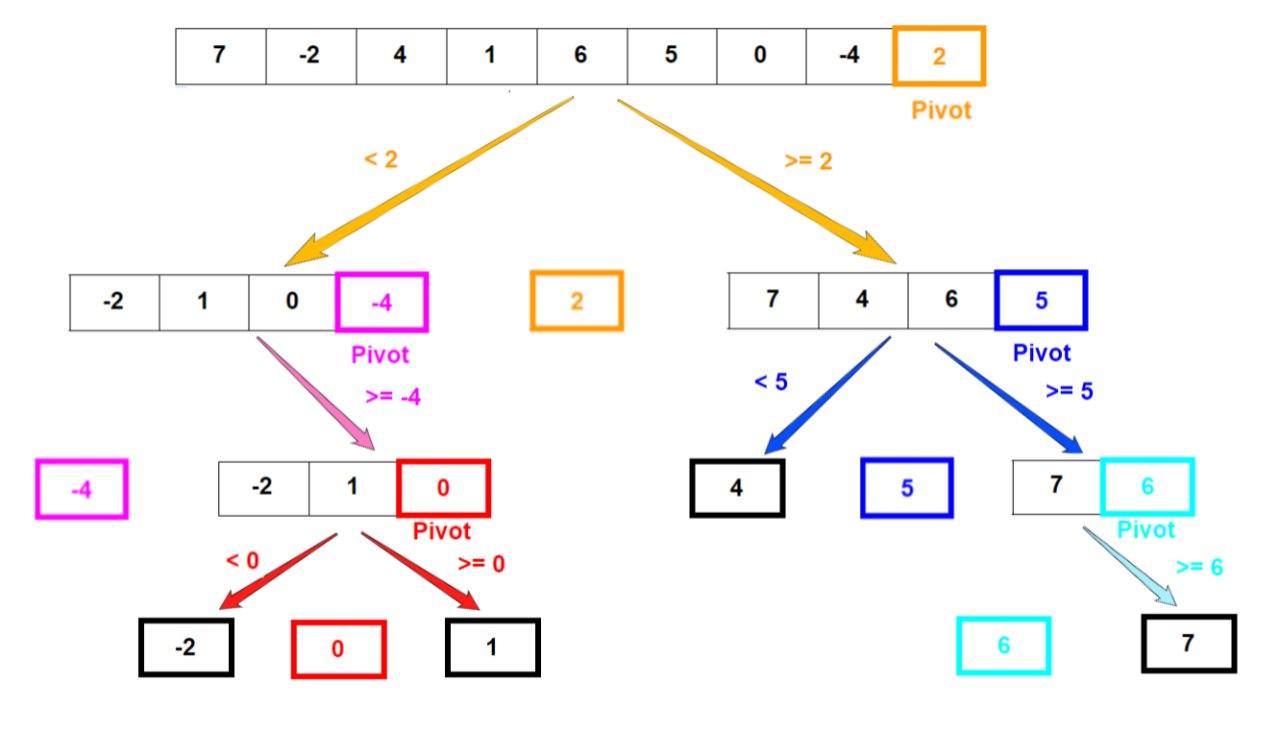Image source: https://stackabuse.com/quicksort-in-javascript/

Link to animation for Quick sort - Link to hackerearth.

Described below is the algorithm for quick sort technique.

quick_sort(arr[], left_index, right_index)

If right_index > left_index

Step 1: Select an element as pivot using strategy of choice
Step 2: Call partition function to creat two subpartitions and get the partition index
Step 3: Call quick_sort for first half:
Step 4: Call quick_sort for second half:


int partition (int arr[], int left_index, int right_index){
  int pivot = arr[right_index];
int pivot_index = right_index;
right_index--; /*pivot exists at the right index*/

while(left_index <= right_index){
  if(arr[left_index] < pivot){
    left_index++;
    continue;
  }
  else if(arr[right_index] > pivot){
    right_index--;
    continue;
  }
  else{
    swap(&arr[left_index], &arr[right_index]);
  }
}

/*Now the left index point to location where pivot must go*/
swap(&arr[left_index], &arr[pivot_index]);
return left_index;
}

void quick_sort_func(int arr[], int left_index, int right_index)
{
if (left_index < right_index) {
  int partition_index = partition(arr, left_index, right_index);

  /*recursively sort first and second halves*/
  quick_sort_func(arr, left_index, partition_index - 1);
  quick_sort_func(arr, partition_index + 1, right_index);
}
}

HOME PREV NEXT